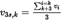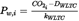[F1Appendix 6
Textual Amendments
Verification of trip dynamic conditions with method 2 (Power Binning) U.K.
1. INTRODUCTION U.K.
This Appendix describes the data evaluation according to the power binning method, named in this appendix ‘ evaluation by normalisation to a standardised power frequency (SPF) distribution ’ .
2. SYMBOLS, PARAMETERS AND UNITS U.K.
[ F2 ]
Reference acceleration for P drive , [0,45 m/s 2 ]
intercept of the Veline from WLTC
Driving resistance coefficients
Time step for instantaneous measurements, minimum resolution 1Hz
Wheel power class, j = 1 to 9
Slope of the Veline from WLTC
Instantaneous mass of the exhaust component ‘ gas ’ at time step i, [g/s]
3-second moving average mass flow of the exhaust gas component ‘ gas ’ in time step k given in 1 Hz resolution [g/s]
Distance-specific emissions for the exhaust gas component ‘ gas ’ [g/km]

Weighted emission value of an exhaust gas component ‘ gas ’ for the subsample of all seconds i with v i < 60 km/h, g/s
Weighted distance-specific emissions for the exhaust gas component ‘ gas ’ for the subsample of all seconds i with v i < 60 km/h, g/km
phase of WLTC (low, medium, high and extra-high), p = 1 – 4
Engine drag power in the Veline approach where fuel injection is zero, [kW]
Maximum rated engine power as declared by the manufacturer, [kW]
Power to overcome road load and inertia of a vehicle at time step i, [kW]
Same as P required,i defined above used in longer equations
Full load power curve, [kW]
Wheel power class limits for class number j, [kW] (P c,j, lower bound represents the lower limit P c,j, upper bound the upper limit)
Wheel power class limits for class j as normalised power value, [-]
Power demand at the vehicle's wheel to overcome driving resistances in time step i [kW]
3-second moving average power demand at the vehicle's wheel to overcome driving resistances in in time step k in 1 Hz resolution [kW]
Power demand at the wheel hub for a vehicle at reference speed and acceleration [kW]
Normalised power demand at the wheel hub [-]
Total time in step i, [s]
Time share of the wheel power class j, [%]
Start time of the WLTC phase p, [s]
End time of the WLTC phase p, [s]
Test mass of the vehicle, [kg]; to be specified per section: real test weight in PEMS test, NEDC inertia class weight or WLTP masses (TM L , TM H or TM ind )
Standardised Power Frequency distribution
Actual vehicle speed in time step i, [km/h]
Reference velocity for P drive , [70 km/h]
3-second moving average of the vehicle velocity in time step k, [km/h].
Textual Amendments
3. EVALUATION OF THE MEASURED EMISSIONS USING A STANDARDISED WHEEL POWER FREQUENCY DISTRIBUTION U.K.
The power binning method uses the instantaneous emissions of the pollutants, m gas, i (g/s) calculated in accordance with Appendix 4.
The m gas, i values shall be classified in accordance with the corresponding power at the wheels and the classified average emissions per power class shall be weighted to obtain the emission values for a test with a normal power distribution according to the following points.
3.1. Sources for the actual wheel power U.K.
[F4The actual wheel power P r,i shall be the total power to overcome air resistance, rolling resistance, road gradients, longitudinal inertia of the vehicle and rotational inertia of the wheels.]
Textual Amendments
When measured and recorded, the wheel power signal shall use a torque signal meeting the linearity requirements laid down in Appendix 2, point 3.2.
As an alternative, the actual wheel power may be determined from the instantaneous CO 2 emissions following the procedure laid down in point 4 of this Appendix.
[F43.2 Classification of the moving averages to urban, rural and motorway U.K.
The standard power frequencies are defined for urban driving and for the total trip (see paragraph 3.4) and a separate evaluation of the emissions shall be made for the total trip and for the urban part. The three second moving averages calculated according to paragraph 3.3 shall therefore be allocated later to urban and extra-urban driving conditions according to the velocity signal (v i ) from the actual second i as outlined in Table 1-1.
Table 1-1
Speed ranges for the allocation of test data to urban, rural and motorway conditions in the power binning method
| Urban | Rural | Motorway | |
|---|---|---|---|
| v i [km/h] | 0 to ≤ 60 | > 60 to ≤ 90 | > 90] |
3.3. Calculation of the moving averages of the instantaneous test data U.K.
Three-second moving averages shall be calculated from all relevant instantaneous test data to reduce influences of possibly imperfect time alignment between emission mass flow and wheel power. The moving average values shall be computed in a 1 Hz frequency:
Where
time step for moving average values
time step from instantaneous test data.
3.4. Set up of the wheel power classes for emission classification U.K.
3.4.1. The power classes and the corresponding time shares of the power classes in normal driving are defined for normalised power values to be representative for any LDV (Table 1-2). U.K.
Table 1-2
Normalised standard power frequencies for urban driving and for a weighted average for a total trip consisting of 1/3 urban, 1/3 road, 1/3 motorway mileage
| Power class No | P c,norm,j [-] | Urban | Total trip | |
|---|---|---|---|---|
| From > | to ≤ | Time share, t C,j | ||
| 1 | – 0,1 | 21,9700 % | 18,5611 % | |
| 2 | – 0,1 | 0,1 | 28,7900 % | 21,8580 % |
| 3 | 0,1 | 1 | 44,0000 % | 43,45 % |
| 4 | 1 | 1,9 | 4,7400 % | 13,2690 % |
| 5 | 1,9 | 2,8 | 0,4500 % | 2,3767 % |
| 6 | 2,8 | 3,7 | 0,0450 % | 0,4232 % |
| 7 | 3,7 | 4,6 | 0,0040 % | 0,0511 % |
| 8 | 4,6 | 5,5 | 0,0004 % | 0,0024 % |
| 9 | 5,5 | 0,0003 % | 0,0003 % | |
The P c,norm columns in Table 1-2 shall be de-normalised by multiplication with P drive , where P drive is the actual wheel power of the tested car in the type approval settings at the chassis dynamometer at v ref and a ref .
P c,j [kW] = P c,norm, j × P drive
Where:
j is the power class index according to Table 1-2
The driving resistance coefficients f 0 , f 1 , f 2 should be calculated with a least squares regression analysis from the following definition:
P Corrected /v = f 0 + f 1 × v + f 2 × v 2
with ( P Corrected /v ) being the road load force at vehicle velocity v for the NEDC test cycle defined in point 5.1.1.2.8 of Appendix 7 to Annex 4a of UNECE Regulation 83 — 07 series of amendments.
TM NEDC is the inertia class of the vehicle in the type approval test, [kg].
3.4.2. Correction of the wheel power classes U.K.
The maximum wheel power class to be considered is the highest class in Table 1-2 which includes (P rated × 0,9). The time shares of all excluded classes shall be added to the highest remaining class.
From each P c,norm,j the corresponding P c,j shall be calculated to define the upper and lower bounds in kW per wheel power class for the tested vehicle as shown in Figure 1.
Figure 1
Schematic picture for converting the normalised standardised power frequency into a vehicle specific power frequency
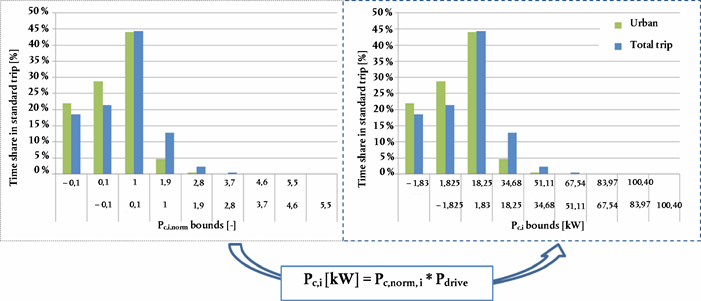
An example for this de-normalisation is given below.
Example for input data:
| Parameter | Value |
|---|---|
| f 0 [N] | 79,19 |
| f 1 [N/(km/h)] | 0,73 |
| f 2 [N/(km/h) 2 ] | 0,03 |
| TM [kg] | 1 470 |
| P rated [kW] | 120 (Example 1) |
| P rated [kW] | 75 (Example 2) |
Corresponding results:
P drive = 70 [km/h]/3,6 × (79,19 + 0,73 [N/(km/h)] × 70[km/h] + 0,03 [N/(km/h) 2 ] × (70 [km/h]) 2 + 1 470 [kg] × 0,45[m/s 2 ]) × 0,001
P drive = 18.25 kW
Table 2
De-normalised standard power frequency values from Table 1-2 (for Example 1)
| a The highest class wheel power class to be considered is the one containing 0,9 × P rated . Here 0,9 × 120 = 108. | ||||
| Power class No | P c,j [kW] | Urban | Total trip | |
|---|---|---|---|---|
| From > | to ≤ | Time share, t C,j [%] | ||
| 1 | All < – 1,825 | – 1,825 | 21,97 % | 18,5611 % |
| 2 | – 1,825 | 1,825 | 28,79 % | 21,8580 % |
| 3 | 1,825 | 18,25 | 44,00 % | 43,4583 % |
| 4 | 18,25 | 34,675 | 4,74 % | 13,2690 % |
| 5 | 34,675 | 51,1 | 0,45 % | 2,3767 % |
| 6 | 51,1 | 67,525 | 0,045 % | 0,4232 % |
| 7 | 67,525 | 83,95 | 0,004 % | 0,0511 % |
| 8 | 83,95 | 100,375 | 0,0004 % | 0,0024 % |
| 9 a | 100,375 | All > 100,375 | 0,00025 % | 0,0003 % |
Table 3
De-normalised standard power frequency values from Table 1-2 ( for Example 2)
| a The highest class wheel power class to be considered is the one containing 0,9 × P rated . Here 0,9 × 75 = 67,5. | ||||
| Power class No | P c,j [kW] | Urban | Total trip | |
|---|---|---|---|---|
| From > | to ≤ | Time share, t C,j [%] | ||
| 1 | All < – 1,825 | – 1,825 | 21,97 % | 18,5611 % |
| 2 | – 1,825 | 1,825 | 28,79 % | 21,8580 % |
| 3 | 1,825 | 18,25 | 44,00 % | 43,4583 % |
| 4 | 18,25 | 34,675 | 4,74 % | 13,2690 % |
| 5 | 34,675 | 51,1 | 0,45 % | 2,3767 % |
| 6 a | 51,1 | All > 51,1 | 0,04965 % | 0,4770 % |
| 7 | 67,525 | 83,95 | — | — |
| 8 | 83,95 | 100,375 | — | — |
| 9 | 100,375 | All > 100,375 | — | — |
3.5. Classification of the moving average values U.K.
Each moving average value calculated according to point 3.2 shall be sorted into the de-normalised wheel power class into which the actual 3-second moving average wheel power P w , 3s,k fits. The de-normalised wheel power class limits have to be calculated according to point 3.3.
The classification shall be done for all three-second moving averages of the entire valid trip data as well as for the all urban trip parts. Additionally all moving averages classified to urban according to the velocity limits defined in Table 1-1 shall be classified into one set of urban power classes independently of the time when the moving average appeared in the trip.
Then the average of all three-second moving average values within a wheel power class shall be calculated for each wheel power class per parameter. The equations are described below and shall be applied once for the urban data set and once for the total data set.
Classification of the 3-second moving average values into power class j (j = 1 to 9):
then: class index for emissions and velocity = j.
The number of 3-second moving average values shall be counted for each power class:
then: counts j = n + 1 (counts j is counting the number of 3-second moving average emission value in a power class to check later the minimum coverage demands).
3.6. Check of power class coverage and of normality of power distribution U.K.
For a valid test the time shares of the single wheel power classes shall be in the ranges listed in Table 4.
Table 4
Minimum and maximum shares per power class for a valid test
| a Representing the total of motoring and low power conditions | ||||||
| P c,norm,j [-] | Total trip | Urban trip parts | ||||
|---|---|---|---|---|---|---|
| Power class No | From > | to ≤ | lower bound | upper bound | lower bound | upper bound |
| Sum 1 + 2 a | 0,1 | 15 % | 60 % | 5 % a | 60 % | |
| 3 | 0,1 | 1 | 35 % | 50 % | 28 % | 50 % |
| 4 | 1 | 1,9 | 7 % | 25 % | 0,7 % | 25 % |
| 5 | 1,9 | 2,8 | 1,0 % | 10 % | > 5 counts | 5 % |
| 6 | 2,8 | 3,7 | > 5 counts | 2,5 % | 0 % | 2 % |
| 7 | 3,7 | 4,6 | 0 % | 1,0 % | 0 % | 1 % |
| 8 | 4,6 | 5,5 | 0 % | 0,5 % | 0 % | 0,5 % |
| 9 | 5,5 | 0 % | 0,25 % | 0 % | 0,25 % | |
In addition to the requirements in Table 4, a minimum coverage of 5 counts is demanded for the total trip in each wheel power class up to the class containing 90 % of the rated power to provide a sufficient sample size.
A minimum coverage of five counts is required for the urban part of the trip in each wheel power class up to class No 5. If the counts in the urban part of the trip in a wheel power class above No 5 are less than five, the average class emission value shall be set to zero.
3.7. Averaging of the measured values per wheel power class U.K.
The moving averages sorted in each wheel power class shall be averaged as follows:
Where
wheel power class 1 to 9 according to Table 1
average emission value of an exhaust gas component in a wheel power class (separate value for total trip data and for the urban parts of the trip), [g/s]
average velocity in a wheel power class (separate value for total trip data and for the urban parts of the trip), [km/h]
time step for moving average values.
3.8. Weighting of the average values per wheel power class U.K.
The average values of each wheel power class shall be multiplied with the time share, t C,j per class according to Table 1-2 and summed up to produce the weighted average value for each parameter. This value represents the weighted result for a trip with the standardised power frequencies. The weighted averages shall be computed for the urban part of the test data using the time shares for urban power distribution as well as for the total trip using the time shares for the total.
The equations are described below and shall be applied once for the urban data set and once for the total data set.
[F43.9. Calculation of the weighted distance-specific emission value U.K.
The time-based weighted averages of the emissions in the test shall be converted into distance-based emissions once for the urban data set and once for the total data set as follows:
Using these formulas, weighted averages shall be calculated for the following pollutants for the total trip and for the urban part of the trip:
weighted NO x test result in [mg/km]
weighted NO x test result in [mg/km]
weighted CO test result in [mg/km]
weighted CO test result in [mg/km]]
4. ASSESSMENT OF THE WHEEL POWER FROM THE INSTANTANEOUS CO 2 MASS FLOW U.K.
The power at the wheels (P w,i ) can be computed from the measured CO 2 mass flow in 1 Hz basis. For this calculation the vehicle-specific CO 2 lines (‘Veline’) shall be used.
The Veline shall be calculated from the vehicle type approval test in the WLTC according to the test procedure described in UNECE Global Technical Regulation No 15 — worldwide harmonised light vehicles test procedure (ECE/TRANS/180/Add.15).
The average wheel power per WLTC phase shall be calculated. in 1 Hz from the driven velocity and from the chassis dynamometer settings. All wheel power values below the drag power shall be set to the drag power value.
With
road load coefficients used in in the WLTP test performed with the vehicle
test mass of the vehicle in the WLTP test performed with the vehicle in [kg]
P drag = – 0,04 × P rated
if P w,i < P drag then P w,i = P drag
The average power per WLTC phase is calculated from the 1 Hz wheel power according to:
With
phase of WLTC (low, medium, high and extra-high)
Start time of the WLTC phase p, [s]
end time of the WLTC phase p, [s].
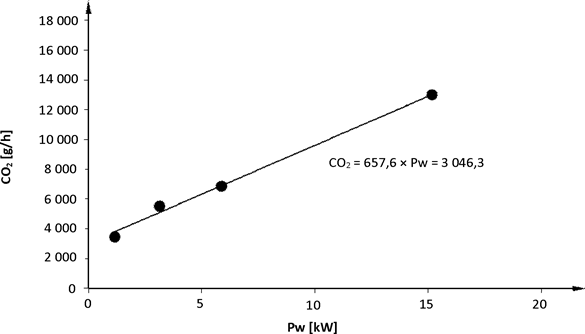
Then a linear regression shall be made with the CO 2 mass flow from the bag values of the WLTC on the y-axis and from the average wheel power P w,p per phase on the x-axis as illustrated in Figure 2.
The resulting Veline equation defines the CO 2 mass flow as function of the wheel power:
Where
slope of the Veline from WLTC, [g/kWh]
intercept of the Veline from WLTC, [g/h].
Figure 2
Schematic picture of setting up the vehicle-specific Veline from the CO 2 test results in the four phases of the WLTC
The actual wheel power shall be calculated from the measured CO 2 mass flow according to:
With
CO 2 in [g/h]
P W,j in [kW]
The above equation can be used to provide P Wi for the classification of the measured emissions as described in point 3 with following additional conditions in the calculation
| if v i < 0,5 and if a i < 0 then P w,i = 0 | v in [m/s] |
| if CO2 i < 0,5 X D WLTC then P w,i = P drag | v in [m/s].] |