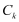Basic equation expressing the equivalence of drawdowns on the one hand and repayments and charges on the other
20.—(1) The basic equation, which establishes the annual percentage rate of charge, equates, on an annual basis, the total present value of drawdowns on the one hand and the total present value of repayments and payments of charges on the other hand, expressed by means of the following formula—
where—
X is the annual percentage rate of charge;
m is the number of the last drawdown;
k is the number of a drawdown thus, 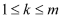


m’ is the number of the last repayment or payment of charges;
l is the number of a repayment or payment of charges;
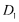

where—
X is the annual percentage rate of charge;
m is the number of the last drawdown;
is the interval between the date of the first drawdown and the date of each subsequent drawdown, thus
;
m’ is the number of the last repayment or payment of charges;
l is the number of a repayment or payment of charges;
is the interval, expressed in years and fractions of a year, between the date of the first drawdown and the date of each repayment or payment of charges.
(2) The following remarks apply to the equation set out in sub-paragraph (1)—
(a)the amounts paid by both parties at different times shall not necessarily be equal and shall not necessarily be paid at equal intervals;
(b)the starting date must be that of the first drawdown;
(c)intervals between dates used in the calculation must be expressed in years or in fractions of a year, where—
(i)a year is presumed to have 365 days (or 366 days for leap years), 52 weeks or 12 equal months; and
(ii)an equal month is presumed to have 30.41666 days regardless of whether or not it is a leap year;
(d)where intervals between dates used in the calculations cannot be expressed as a whole number of weeks, months or years, the intervals must be expressed as a whole number of one of those periods in combination with a number of days;
(e)for the purposes of paragraph (d), where using days—
(i)every day must be counted, including weekends and holidays;
(ii)equal periods and then days must be counted backwards to the date of the initial drawdown; and
(iii)the length of the period of days must be—
(aa)obtained excluding the first day and including the last day; and
(bb)expressed in years by dividing this period by the number of days (365 or 366 days) of the complete year counted backwards from the last day to the same day of the previous year;
(f)the result of the calculation must be expressed with an accuracy of at least one decimal place and if the figure at the following decimal place is greater than or equal to 5, the figure at the preceding decimal place must be increased by one;
(g)the equation may be rewritten using a single sum and the concept of flows (
where s is the present balance of flows;
(h)for the purposes of paragraph (g), if the aim is to maintain the equivalence of flows, the value of s will be zero.